Le test de Student :
comparer deux moyennes avec rigueur,
sans surinterpréter

Comparer la satisfaction moyenne de deux segments, vérifier si une population « client » se distingue réellement d’une population « prospect »… Dans la plupart des cas, la réponse passe par un outil simple et efficace, le test de Student, souvent appelé t-test. Ce test est complémentaire au test de Fisher.

Dans cet article découvrez comment l’appliquer et l’interpréter.

I – Quand le test de Student est le bon outil (et quand il ne l’est pas)

Le test de Student répond à une question précise : la moyenne d’une variable quantitative est-elle différente entre deux groupes, au-delà de ce que l’aléa d’échantillonnage peut produire ?

Ainsi, ce test devient pertinent dès que vous comparez des scores ou des mesures comme une note de satisfaction sur 10, un score d’image sur 5, un indice construit à partir de plusieurs items, une durée moyenne, un montant moyen, etc.

En revanche, dès que vous quittez cette logique « deux groupes / une moyenne », il faut changer d’outil. En effet, si vous comparez plus de deux groupes (par exemple quatre régions), vous vous exposez à multiplier les tests et donc à générer des faux positifs. Dans ce cas précis, une ANOVA est plus appropriée.

Si vous comparez des proportions, par exemple le pourcentage de satisfaits, le test de Student n’est pas adapté. En effet, il convient d’utiliser plutôt un test de proportions ou un chi², selon le cas. Enfin, si vous cherchez à attribuer un effet ou à identifier des leviers explicatifs, vous aurez besoin d’un modèle (régression, drivers, etc.) et non pas d’un test de Student isolé.

II – Les trois versions du test de Student

Le terme du « test de Student » est le plus couramment employé, mais en pratique, trois situations reviennent.

a) La comparaison de deux groupes indépendants

La première est la comparaison de deux groupes indépendants, composés de répondants différents : clients versus prospects, hommes versus femmes, etc. C’est la situation la plus fréquente en études lorsque vous devez faire un test sur deux échantillons différents.

b) La mesure « avant/après »

La deuxième situation est celle d’une mesure « avant/après » sur les mêmes individus (ou de deux mesures sur un même panel), par exemple une évaluation avant test puis après test. Dans ce cas, il n’y a pas deux groupes indépendants mais des paires. Le bon outil est alors le test de Student apparié, qui travaille sur les différences individuelles. Il est généralement plus puissant, car il neutralise une partie de la variabilité inter-individuelle.

c) la variabilité incomparable

La troisième situation concerne l’hypothèse, souvent implicite, que la variabilité au sein de chaque groupe ne soit pas comparable. Cependant, c’est loin d’être garanti dans la mesure où deux segments peuvent avoir des dispersions très différentes, et les tailles de groupe sont rarement parfaitement équilibrées. C’est précisément pour cela qu’il existe le t-test de Welch, une variante du t-test indépendant qui ne suppose pas l’égalité des variances.

III – Avant de lancer le test : les vérifications qui évitent les conclusions bancales

Le test de Student n’est pas une formule magique, il s’agit d’un test statistique qui amplifie la qualité ou les défauts de tes données. Trois contrôles rapides font gagner du temps et évitent les mauvaises surprises.

a) Comparez une moyenne sur une variable quantitative

D’abord, assurez vous que vous comparez bien une moyenne sur une variable traitable comme quantitative. En études, on utilise souvent le t-test sur des notes 0–10, des scores 1–5 ou des indices composites. C’est acceptable dans la plupart des contextes opérationnels, mais il faut en assumer la logique : vous testez une différence de score moyen, pas une vérité absolue sur une « mesure continue parfaite ». Ainsi, plus l’effectif est faible, plus cette approximation exige de prudence.

b) vérifiez toujours la structure de vos groupes

Ensuite, vérifiez toujours la structure de vos groupes. En effet, un répondant ne doit appartenir qu’à un seul groupe si vous faites un test indépendant. Si vous êtes en « avant/après », ne traitez pas cela comme deux groupes indépendants car vous perdrez l’information de couplage et risquez de conclure à tort.

c) Contrôlez les points de qualité de données

Enfin, contrôlez bien les points de qualité de données qui perturbent les moyennes. En effet, les valeurs hors plage, les erreurs de codage et les valeurs aberrantes peuvent fabriquer une différence ou la masquer. Un petit segment avec quelques réponses extrêmes suffit à faire basculer un résultat, surtout sur des effectifs modestes. L’enjeu n’est donc pas de « nettoyer pour que ça marche », mais de documenter ce que vous faites et pourquoi vous le faites, afin que votre analyse soit défendable.

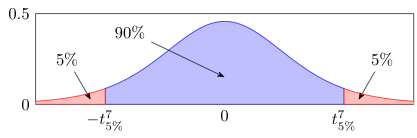
Le test de Student

IV – Comment le formuler dans un rapport : des phrases de restitution crédibles

Si vous avez un résultat significatif, vous devez alors mentionner :

• les moyennes,
• l’écart,
• l’intervalle de confiance,
• la p-value.

Par exemple, si la satisfaction moyenne est plus élevée chez les clients que chez les prospects, avec un écart de +0,4 point, alors l’intervalle de confiance est à 95% et suggère que l’écart réel se situe probablement entre +0,08 et +0,72

Ensuite, vous pouvez ajouter une phrase métier du type : « l’effet est modéré ou faible, et son intérêt opérationnel dépend du seuil de différence minimale retenu ».

Si le résultat n’est pas significatif, il faut éviter le piège « donc il n’y a pas de différence ». En effet, il convient plutôt de dire : « un écart est observé, mais il n’est pas possible d’écarter l’hypothèse d’une différence nulle au seuil choisi. L’intervalle de confiance recouvre 0, ce qui indique que, compte tenu de l’incertitude, plusieurs scénarios restent plausibles. » Cette posture protège ainsi ton étude et évite les contresens.

V – Exemple : mise en œuvre d’un test de Student en enquête de satisfaction

a) Contexte de l’étude

Dans le cadre d’une enquête de satisfaction annuelle, notre institut d’études souhaite comparer la satisfaction globale moyenne entre deux segments : les clients actifs et les prospects qualifiés.
L’objectif est clairement défini en amont : vérifier si l’expérience effective du service se traduit par un niveau de satisfaction significativement plus élevé chez les clients.

b) Description des données

Après nettoyage des données, les résultats descriptifs sont les suivants :

• Clients : 200 répondants, satisfaction moyenne de 7,3 sur 10, écart-type de 1,5
• Prospects : 190 répondants, satisfaction moyenne de 7,0 sur 10, écart-type de 1,6

Les tailles d’échantillon sont comparables et les dispersions très proches. L’examen des distributions ne révèle ni asymétrie marquée ni valeurs aberrantes susceptibles d’influencer excessivement les moyennes.

Dans ce contexte, l’hypothèse d’égalité des variances est jugée raisonnable. Le plan d’analyse prévoit donc l’utilisation d’un test de Student pour échantillons indépendants, bilatéral, avec un seuil de significativité de 5 %.

c) Formulation des hypothèses

L’hypothèse nulle pose l’égalité des moyennes de satisfaction entre clients et prospects.
L’hypothèse alternative considère qu’une différence existe entre les deux groupes.

Même si une satisfaction plus élevée est attendue chez les clients, le test reste bilatéral afin de conserver une approche prudente et standard en étude.

d) Résultats du test

Le test de Student met en évidence une différence de moyennes de +0,3 point en faveur des clients.
L’intervalle de confiance à 95 % de cette différence est compris entre +0,06 et +0,54 point, et la p-value associée est de 0,015.

Ces résultats conduisent au rejet de l’hypothèse nulle dans la mesure où l’écart observé est statistiquement significatif au seuil de 5 %.

e) Interprétation

Un écart de +0,3 point sur une échelle de 0 à 10 correspond, dans cette étude, au seuil minimal de différence jugée pertinente lors du cadrage. L’effet existe donc, mais reste modéré. Il confirme une tendance attendue plutôt qu’il ne révèle une rupture forte entre clients et prospects.

f) Exemple de restitution dans le rapport

Une formulation rigoureuse et équilibrée pourrait être la suivante :

« La satisfaction moyenne est légèrement plus élevée chez les clients (7,3) que chez les prospects (7,0), soit un écart de +0,3 point. Cette différence est statistiquement significative (test de Student, p = 0,015). L’intervalle de confiance à 95 % indique que l’écart réel se situe probablement entre +0,06 et +0,54 point. L’effet observé est modéré et correspond au seuil minimal d’intérêt défini pour l’étude. »

Rédigé par :

Séverine PICHOLLET Directrice d’études chez Le Sphinx Domaines d’expertise : dispositifs d’écoute client, enquête notoriété-image, gestion de panel et tests produits, enquêtes RH (climat interne, RPS) Séverine évolue depuis plus de 15 ans au sein de l’Institut Sphinx, où elle a développé une expertise approfondie dans le secteur des Assurances et Mutuelles. Elle conçoit et met en œuvre des dispositifs d’enquêtes adaptés pour répondre aux enjeux stratégiques de ces acteurs. Par ailleurs, elle assure la gestion et le développement des relations avec une clientèle grands comptes.