Institut
25 octobre 2024
Blog
#Tests statistiques
#Analyse
#bivariée
L’objectif d’une analyse bivariée est d’étudier les relations entre 2 variables. Elle permet de savoir s’il y a un lien entre les réponses qui sont faites à 2 questions différentes.
En fonction des 2 variables à croiser, un test statistique particulier est à mettre en œuvre afin d’étudier au mieux la relation entre ces 2 variables. Cependant, le choix du test dépend de la nature des variables.
Quelle que soit la nature des variables étudiées, une analyse croisée doit passer par trois niveaux d’interprétation :
- D’abord, l’étude de l’existence de la relation entre les deux variables,
- Ensuite, si relation il y a, celle-ci est-elle moyenne, forte ou très forte.
- Enfin, comment se traduit-elle dans les faits ?
Dans cet article nous vous expliquons les 3 principaux tests statistiques, et comment interpréter les résultats avec un exemple concret d’application.
I – Le test du Chi²
a) Définition du test du Chi²
Le test du Chi² est le croisement de 2 variables fermées avec des catégories. Il permet de savoir si ces variables sont interdépendantes, c’est-à-dire s’il y a un lien entre les deux. Il se base sur la comparaison d’effectifs réels avec des effectifs théoriques.
Si la différence entre ces deux fréquences est significative, nous pouvons conclure qu’il existe une relation entre les deux variables étudiées, et que les différences ne sont probablement pas dues au hasard.
b) Interpréter les résultats d’un test du Chi²
Pour bien interpréter les résultats d’un test du Chi², il convient de comparer le Chi² calculé à une valeur repère à dépasser, qui est le Chi² théorique.
Ainsi, si la valeur du Chi² calculé est supérieure à la valeur du Chi² théorique, alors il existe une relation entre les deux variables avec un risque d’erreur p (p étant la probabilité de se tromper en affirmant que la relation est significative).
Pour juger de la force de la relation, il faut ensuite comparer les valeurs du Chi² théorique en baissant progressivement le taux d’erreur p. Si le Chi² calculé reste significatif, cela traduit la force de la relation. Ainsi, plus l’écart est grand, plus le Chi² est élevé, et plus la relation entre les deux variables est forte.
c) Exemple d’application
Prenons l’exemple d’un tableau croisé qui représente le degré de satisfaction par note de recommandation (promoteurs, neutres, détracteurs). Nous nous retrouvons avec le tableau suivant :
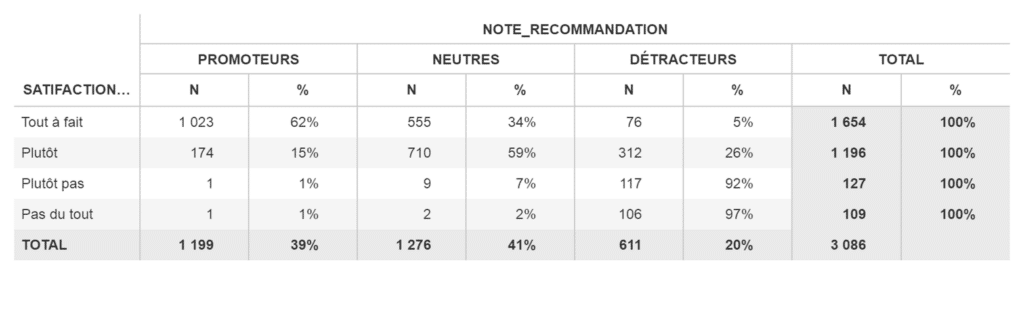
Le test du Chi² peut être utilisé ici pour vérifier s’il existe un lien entre la satisfaction et la note de recommandation. Dans ce cas, nous calculons les fréquences attendues pour chaque catégorie (le N TH, nombre théorique) en supposant que la note de recommandation et la satisfaction sont indépendantes. Nous arrivons sur le tableau suivant :
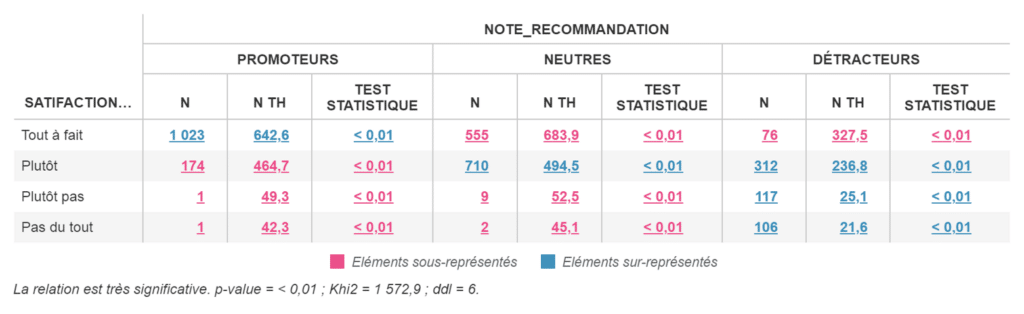
Ici, nous nous retrouvons avec un Chi² calculé de 1572.9 et un Chi2 théorique de 24.10. La valeur du risque d’erreur p étant inférieure à 0.01, le résultat du test de Chi² est donc très significatif !
Nous pouvons donc conclure qu’il existe bien un lien fort entre la satisfaction et la note de recommandation.
II – Test de Fisher
a) Définition du test de Fisher
Le test de Fisher est utilisé dans le cadre d’une analyse croisée d’une variable fermée avec catégories avec une variable numérique. Il permet de comparer les moyennes en se basant sur l’analyse de la variance.
Avec un test de Fisher, nous cherchons à savoir s’il y a davantage de différences entre les groupes (variance inter groupe) qu’à l’intérieur de chaque groupe (variance intra groupe). Le rapport entre ces deux variances est alors appelé F.
Si la différence entre les moyennes est significative, nous pouvons conclure qu’il existe une relation entre les deux variables étudiées, et que les différences ne sont probablement pas dues au hasard.
b) Interpréter les résultats d’un test de Fisher
Pour interpréter le résultat d’un test de Fisher, il convient de comparer le résultat obtenu (F) à une valeur repère à dépasser, qui est le F théorique. Si la valeur du F calculé est supérieure à valeur du F théorique, il existe alors une relation entre les deux variables avec un risque d’erreur p (p est la probabilité de se tromper en affirmant que la relation est significative).
Pour juger de la force de la relation, il faut comparer les valeurs du F théorique en baissant progressivement le risque d’erreur p (dans la table statistique). Si le F calculé reste significatif, ceci traduit la force de la relation.
c) Exemple d’application du test de Fisher
Prenons un exemple où nous souhaitons savoir s’il existe une relation significative entre les origines d’une voiture (Française, Allemande…) et leur fiabilité (note sur 20).
Voici les données sous forme de tableau :
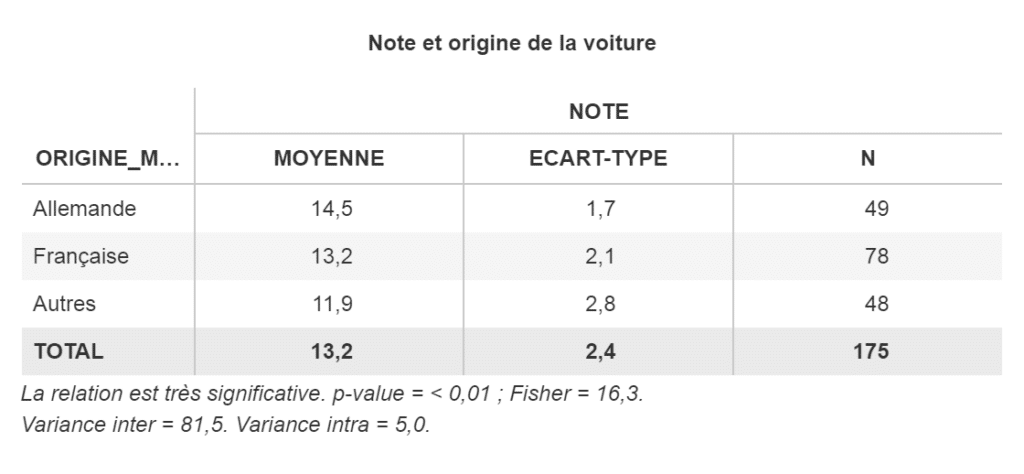
Dans l’exemple ci-dessus, le F calculé est à 16.3 et le F théorique est à 3.8 avec un risque d’erreur à 1%. Donc nous avons bien une relation car le F calculé est largement supérieur au F théorique
III – Test de corrélation
a) Définition du test de corrélation
Le test de corrélation permet de mesurer la relation entre deux variables numériques. Il permet de déterminer si ces deux variables évoluent ensemble (relation positive), de manière opposée (relation négative), ou si elles sont indépendantes l’une de l’autre (absence de corrélation).
La technique mise en œuvre permet d’obtenir un nuage de points et une droite de régression des deux variables.
Le test de corrélation permet par exemple d’analyser la relation entre la satisfaction client (note sur 10) et la fréquence d’achat (nombre d’achats par mois).
b) Interpréter les résultats d’un test de corrélation
Le coefficient de corrélation, généralement symbolisé par « r », varie entre -1 et 1.
Ainsi, si r est :
- Proche de +1, la corrélation est très forte, et les deux variables varient dans le même sens
- Proche de -1, la corrélation est très forte, et les variables varient dans un sens inverse
- Proche de 0, la corrélation est nulle, il n’y a donc aucun lien entre les deux variables.
c) Exemple d’application
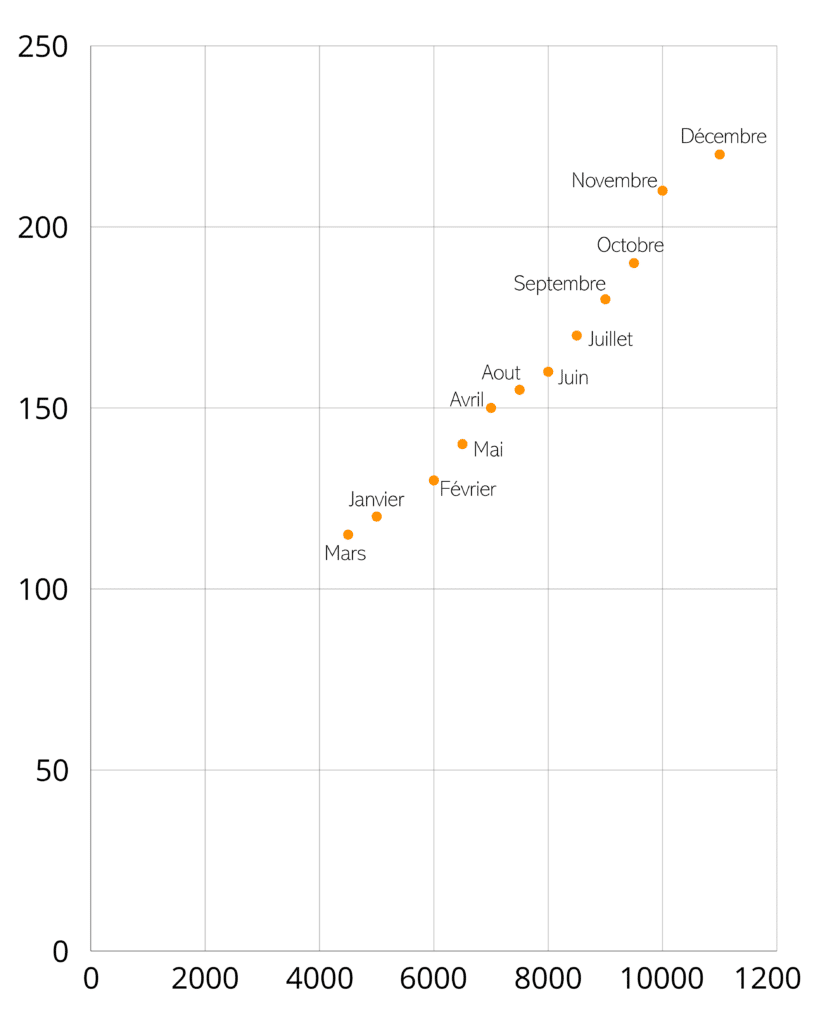
Imaginons que vous soyez responsable marketing d’une entreprise et que vous vouliez analyser la relation entre vos dépenses en publicité en ligne et l’évolution de vos ventes mensuelles. Le but est de savoir si l’augmentation des dépenses publicitaires impacte positivement vos ventes.
Supposons que vous disposiez des données suivantes sur une période de 12 mois :
| Mois | Dépenses en publicité | Ventes (en unités) |
| Janvier | 5000 € | 120 |
| Février | 6000 € | 130 |
| Mars | 4500 € | 115 |
| Avril | 7000 € | 150 |
| Mai | 6500 € | 140 |
| Juin | 8000 € | 160 |
| Juillet | 8500 € | 170 |
| Août | 7500 € | 155 |
| Septembre | 9000 € | 180 |
| Octobre | 9500 € | 190 |
| Novembre | 10000 € | 210 |
| Décembre | 11000 € | 220 |
En appliquant un test de corrélation, nous obtenons un coefficient de 0,95. Cela signifie qu’il y a une forte corrélation positive entre les dépenses publicitaires et les ventes. Plus vous investissez dans la publicité, plus vos ventes augmentent.
Cette corrélation forte suggère ainsi que l’investissement publicitaire joue un rôle important dans la performance des ventes. Cependant, il est essentiel de noter que la corrélation n’implique pas nécessairement une relation de causalité. D’autres facteurs peuvent influencer cette relation.
Vous souhaitez être accompagné et conseillé pour mettre en place des tests statistiques et comprendre les relations entre vos données ? Nos charges d’études sont à votre disposition !
Rédigé par :
À lire aussi
Les analyses multivariées : exemples et définitions
Lorsque vous souhaitez étudier simultanément plus de deux informations, soit plus de deux variables à la fois, il est nécessaire d'utiliser les analyses dites « multivariées ».

10 façons d‘analyser une question fermée à choix multiple ordonnés
Lors de la création de votre étude, il peut être intéressant de proposer à vos répondants une question fermée à choix multiple ordonnés. En effet, celle-ci vous permettra de retirer un nombre important d'enseignements. Découvrez comment analyser les réponses.

Les différents indicateurs pour réaliser une analyse de sentiment
Analyser le sentiment exprimé dans un commentaire permet d'identifier si le répondant est globalement satisfait ou insatisfait en fonction des mots et des expressions qu'il utilise. Plusieurs méthodes existent pour effectuer cette analyse.