Comment déterminer la marge d’erreur
dans une enquête ?

Vous avez obtenu 62 % de satisfaction dans votre enquête. Mais cette valeur est-elle vraiment fiable ? Pour le savoir, il faut comprendre la marge d’erreur, indicateur clé de la précision de vos résultats. Elle permet de savoir jusqu’où vos conclusions peuvent varier en fonction de la taille d’échantillon, du niveau de confiance et de la variabilité des réponses.

I – Pourquoi la marge d’erreur est essentielle ?

Une enquête, aussi bien conçue soit-elle, repose toujours sur un échantillon et non sur l’ensemble de la population étudiée. Cette approche crée ainsi une incertitude statistique : les résultats observés sur l’échantillon sont-ils conformes à ceux qui auraient été observés sur l’ensemble de la population ?

C’est là qu’intervient la notion de marge d’erreur. En effet, celle-ci définit un intervalle de confiance autour d’un résultat, exprimé sous la forme : Résultat ± marge d’erreur

Par exemple, si 52 % des répondants déclarent être satisfaits, avec une marge d’erreur de ± 3 %, cela signifie que le vrai taux de satisfaction dans la population se situe probablement entre 49 % et 55 %.

Attention, il est important de préciser que la marge d’erreur ne prend pas en compte les biais tels que les biais d’échantillonnage. Elle suppose un échantillon aléatoire simple

II – Qu’est-ce que la marge d’erreur ?

a) Définition

La marge d’erreur mesure donc la variabilité naturelle d’un échantillon. Elle dépend de trois éléments principaux :

1. de la taille de l’échantillon (n),
2. de la proportion observée (p),
3. et du niveau de confiance (Z) choisi.

Plus votre échantillon est petit ou votre niveau de confiance élevé, plus la marge d’erreur augmente.

b) Le rôle du niveau de confiance

Le niveau de confiance indique la probabilité que le résultat réel se trouve dans l’intervalle calculé.

Les plus utilisés sont :

Autrement dit, un intervalle de confiance à 95 % signifie que si l’on répétait 100 fois la même enquête, 95 fois sur 100 les résultats se situeraient dans l’intervalle défini.

Précision : ces valeurs valent pour une loi normale bilatérale (des deux côtés de l’intervalle).

III – Comment calculer la marge d’erreur

a) La formule de base

La formule mathématique pour calculer la marge d’erreur dans une enquête est :

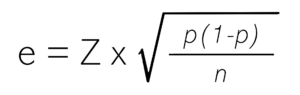
Dans cette formule :

• e = marge d’erreur,
• Z = coefficient du niveau de confiance,
• p = proportion observée (ex. : 0,5 pour 50 %),
• n = taille de l’échantillon.

b) Exemple concret

Par exemple, une enquête menée auprès de 400 personnes montre que 50 % des répondants sont satisfaits. En prenant un niveau de confiance de 95 %, nous obtenons alors :

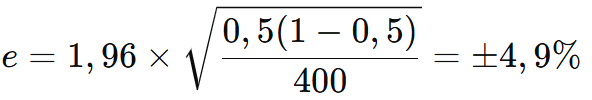
Le résultat réel se situe donc probablement entre 45,1 % et 54,9 % : On ajoute et on soustrait à notre résultat la marge d’erreur, afin d’obtenir un intervalle de confiance dans lequel se situe notre résultat. On retrouve ici la notion de bilatéralité.

c) Comprendre l’influence des paramètres

• Taille d’échantillon (n) : l’erreur diminue à mesure que l’échantillon augmente (mais de façon non linéaire). Donc plus votre échantillon est important, plus votre marge d’erreur diminue.
• Proportion observée (p) : la marge d’erreur est maximale quand p = 0,5.
• Niveau de confiance (Z) : plus le niveau est élevé (ex. : 99 %), plus l’erreur augmente.

Doubler la taille d’échantillon ne divise pas la marge d’erreur par deux : il faut la multiplier par la racine carrée du rapport.

IV – Quelle marge d’erreur est « acceptable » ?

Tout dépend de l’objectif et du contexte de votre étude. Voici quelques repères pratiques pour vous aider, sur la base d’un niveau de confiance à 95 % :

Précision : Pour des petits échantillons (n < 30), on devrait employer la loi de Student (t) plutôt que la loi normale.

Ainsi, une marge d’erreur inférieure à 3 % est idéale pour des études à fort enjeu stratégique, tandis qu’une marge jusqu’à 10 % peut être acceptable pour des explorations ou des publics difficiles à atteindre.

V – Et pour les moyennes, la marge d’erreur s’applique aussi ?

Oui ! La marge d’erreur ne concerne pas que les pourcentages, elle s’applique également aux moyennes (notes de satisfaction, indices de perception, scores d’image, etc).

La formule adaptée pour calculer la marge d’erreur d’une moyenne est alors :

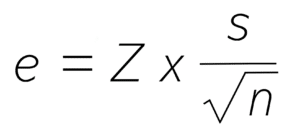
où « s«  représente l’écart-type observé.

Par exemple, vous avez une note moyenne de satisfaction de 7,2/10, avec un écart-type de 1,8 pour un échantillon de 200 personnes.

Votre marge d’erreur est alors de : e = 1,96 × (1,8 / √200) = ± 0,25.

Donc votre vraie moyenne se situe entre 6,95 et 7,45.

Dans Sphinx iQ3, ce calcul est automatisé. En effet, le logiciel affiche directement les intervalles de confiance autour des résultats, garantissant une lecture rigoureuse des écarts significatifs.

Attention : Pour n < 30, utiliser la valeur de t (loi de Student) au lieu de Z.

L’astuce du Sphinx :

Évitez d’interpréter des écarts plus petits que la marge d’erreur et de comparer des sous-échantillons trop faibles (< 50 répondants). En dessous de 30 observations, les intervalles de confiance deviennent trop larges pour des interprétations robustes. Nous vous conseillons également de toujours mentionner la précision statistique dans vos communications des résultats. Cela attestera du sérieux de votre analyse.

Rédigé par :

Marion CHIPEAUX Chargée d’études chez Le Sphinx Domaines d’expertise : Psychologie, Méthodologie d’enquête par questionnaire et Traitement statistique de données quantitatives. Après plusieurs années passées dans le monde académique en tant que chercheuse en Psychologie sociale au sein de l’Université de Genève, Marion Chipeaux a rejoint l’équipe du Sphinx afin de mettre ses compétences méthodologiques et son expertise en matière de comportements humains au service des entreprises soucieuses d’optimiser et de maintenir la satisfaction de leurs clients, ainsi que le bien-être de leurs employés.