Quelle est la taille d'échantillon nécessaire
pour obtenir des résultats significatifs ?

Quelle est la taille d’échantillon nécessaire pour obtenir des résultats significatifs ?

La taille d’échantillon correspond au nombre d’individus interrogés dans une étude ou un sondage afin d’obtenir des résultats statistiquement fiables. Elle dépend principalement de trois paramètres :

• le niveau de confiance (souvent 95 %),
• la marge d’erreur acceptable,
• la variabilité de la population étudiée.

Une taille d’échantillon insuffisante peut conduire à des résultats non significatifs, tandis qu’un échantillon surdimensionné augmente inutilement les coûts d’enquête. Dans ce guide complet, nous expliquons :

• comment calculer la taille d’échantillon,
• quelles formules utiliser selon votre type d’étude,
• quels sont les seuils recommandés en pratique,
• et comment éviter les erreurs fréquentes en sondage.

Que vous réalisiez une étude marketing, une enquête RH ou une recherche académique, comprendre le calcul de la taille d’échantillon est indispensable pour garantir la fiabilité de vos résultats.

I – Qu’est-ce que la taille d’un échantillon ?

a) Définition

La taille de l’échantillon fait référence au nombre d’individus que vous sélectionnez pour participer à votre étude. Elle joue un rôle crucial dans la généralisation des résultats de votre échantillon à une population plus large. Une taille d’échantillon appropriée garantit que vos conclusions seront représentatives et fiables.

Ainsi, si votre échantillon est trop grand, cela peut créer des coûts logistiques inutiles et des retards dans la restitution de vos résultats. En revanche, si votre échantillon est trop petit, les résultats obtenus ne pourront pas être statistiquement significatifs, et vous n’en tirerez alors aucune conclusion fiable.

b) Le rôle de la variabilité

La variabilité au sein de la population que vous étudiez influence la taille de l’échantillon requise. Si votre population présente une grande variabilité, vous aurez alors besoin d’un échantillon plus important pour capturer cette diversité et obtenir des résultats significatifs.

L’écart-type est la mesure de variabilité la plus couramment utilisée pour les moyennes. Il nous indique à quel point chacune de nos observations est proche de la moyenne. Un écart-type plus important indique ainsi que nos données sont plus étalées.

c) Le niveau de confiance et la marge d’erreur

Dans les études statistiques, le niveau de confiance représente le niveau de certitude accordé aux résultats d’une enquête, et est exprimé en pourcentage. Il s’agit d’une plage de valeur à l’intérieur de laquelle se situe à coup sûr (généralement à 95% dans les études marketing) le résultat réel.

La marge d’erreur exprime quant à elle l’étendue et l’écart que les résultats peuvent avoir si vous deviez mener à nouveau la même enquête.

La taille de l’échantillon est ainsi étroitement liée au niveau de confiance que vous souhaitez atteindre dans vos résultats. Plus vous désirez un niveau de confiance élevé, plus votre échantillon doit être grand. De même, la marge d’erreur que vous pouvez tolérer affecte également la taille de l’échantillon. Une marge d’erreur plus faible nécessite un échantillon plus important.

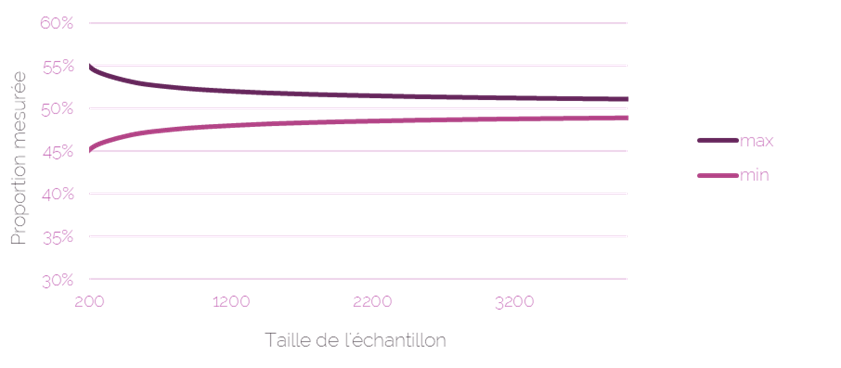
Précision statistique selon la taille de l’échantillon

II – Calculer la marge d’erreur d’un sondage

Au sein de l’Institut Le Sphinx, recueillir des réponses de bonne qualité constitue sans nul doute l’une des préoccupations centrales du chargé d’étude. Cependant, qu’est-ce que qu’une réponse « de bonne qualité » ?

Lors d’une diffusion d’une enquête par questionnaire, les risques d’erreurs potentiels sont bien présents. En effet, si certaines phases de l’enquête sont mal paramétrées (mauvaise rédaction du questionnaire, mauvais choix des interviewés, mauvaise collecte des données…), et comme de fait, nous n’interrogeons pas l’exhaustivité de la population, les réponses ne seront pas réellement exploitables.

Mais ne vous inquiétez pas, nous allons vous expliquer comment réduire au maximum l’erreur d’estimation de votre étude !

a) Prérequis pour calculer la précision de votre échantillon

Dans le cas du sondage « pur », deux conditions doivent être préalablement remplies :

• la taille de l’échantillon (n) doit être inférieure à 1/7, soit environ 15%, de la taille de la population mère (N),
• la taille de l’échantillon (n) doit être supérieur à 30.

b) Les formules pour calculer les erreurs d’estimation d’une enquête

Pour calculer une moyenne

Si vous souhaitez calculer votre marge d’erreur sur une moyenne, la formule est :

e = 1.96 x (ơ/√n)

ơ étant l’écart type et n la taille de l’échantillon.

Exemple

Vous interrogez un échantillon de 500 français. Vous souhaitez connaître le temps moyen passé par jour à regarder la télévision. Le résultat de l’étude est de 200 minutes par jour. L’écart type est de 45 minutes.
L’erreur d’estimation est alors de : 1.96 x (45/ √500) = 3.94 minutes, soit 4 minutes !

Donc pour l’ensemble des Français, le temps moyen passé à regarder la télévision est compris entre 196 et 204 minutes par jour !

Pour calculer un pourcentage ou une proportion

Si vous souhaitez connaitre l’erreur d’estimation sur une enquête ayant pour résultat un pourcentage, alors la formule pour estimer votre erreur est :

e = 1.96 x √[(p x (1 – p) / n)]

Exemple

Vous interrogez un échantillon de 1 500 Français, dont 30% d’entre eux sont satisfaits de l’action du gouvernement.

Votre erreur d’estimation sera alors de : 1,96 x √[(0,3 x (1 – 0,3) / 1500)] = 0.023, soit 2.3 points !

Ainsi, pour l’ensemble des Français, le pourcentage des personnes satisfaites de l’action du gouvernement est alors compris entre 27.7% et 32.3% !

💡Ces deux formules magiques vous permettront ainsi de calculer avec précision la marge d’erreur de votre sondage, et d’avoir des résultats au plus proche de la réalité !

III – Définir la taille minimale d’un échantillon

a) La formule

À une taille d’échantillon donnée est associée une erreur d’estimation. Pour calculer la taille minimale d’un échantillon (n) à partir de l’erreur d’estimation (e), il convient d’appliquer la formule suivante :

n = (p x 1-p)/(e/1.96)²

p, étant la proportion observée en %, il est en effet préférable de faire nos hypothèses sur p=50% (0,5). En effet, c’est la valeur pour laquelle le risque d’erreur est le plus important.

La formule à appliquer est donc :

n=0.25/(e/1.96)²

Exemple
Vous souhaitez mettre en place une sondage politique sur un échantillon de Français. Sachant que l’élection présidentielle à venir s’annonce particulièrement serrée et indécise, vous souhaitez travailler avec une erreur maximale de 1 point.

Vous devrez alors interroger : n=0.25/(0.01/1.96)2 = 9 604 personnes !

b) précisions

L’erreur maximal d’estimation n’est pas directement proportionnelle à la taille de l’échantillon. En effet, il ne suffit pas de doubler la taille de l’échantillon pour doubler sa précision. Schématiquement, pour multiplier par deux sa précision, il faudra multiplier par 4 la taille de l’échantillon.

Les sondages nationaux portent souvent sur des échantillons d’un millier de personnes. C’est en effet à ce niveau que se situe le meilleur rapport précision/taille, qui équivaut au rapport qualité/prix d’un échantillon pour un institut de sondage, comme le représente l’illustration ci-dessous.

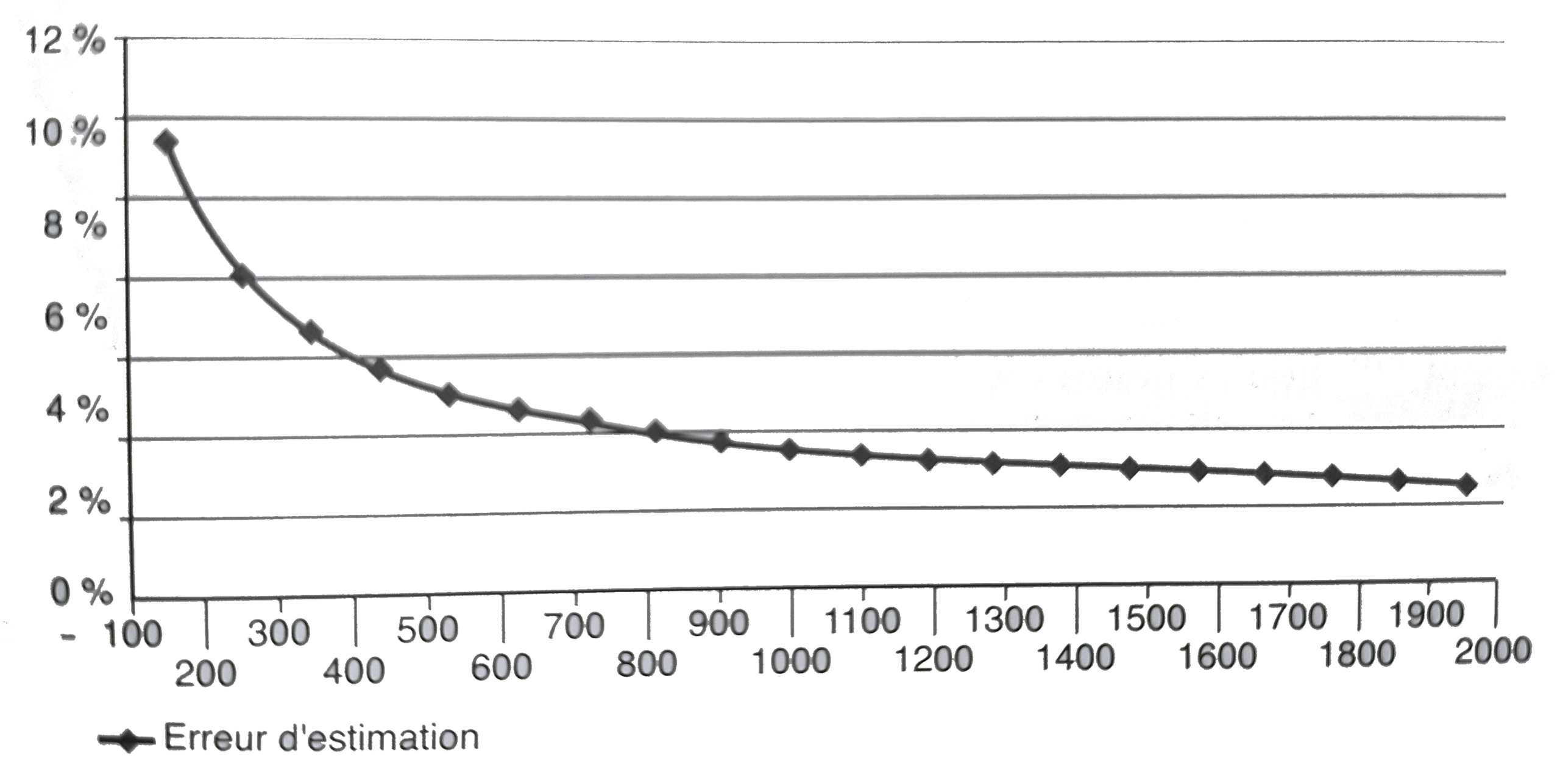
Marge de l’erreur en fonction de la taille de l’échantillon

Conclusion

La taille de l’échantillon est un aspect essentiel de la recherche scientifique et des enquêtes. Elle détermine la validité et la fiabilité de vos résultats, et par conséquent, leur utilité et leur impact. Lorsque vous planifiez une enquête ou un sondage, prenez le temps nécessaire pour déterminer la structure et la taille de votre échantillon. Vous pouvez également vous appuyer sur l’expertise d’un institut d’études, qui saura vous conseiller sur la constitution d’un échantillon optimal par rapport à la problématique de votre étude.

Avec ou sans institut, en s’appuyant sur des méthodes appropriées et en tenant compte des facteurs pertinents, vous pouvez garantir que vos résultats seront dignes de confiance. En fin de compte, une taille d’échantillon bien choisie renforce la crédibilité de votre étude et la qualité de vos conclusions.

FAQ – Taille d’échantillon

1. Quelle est la taille d’échantillon idéale pour un sondage ?

2. Comment calculer la taille d’un échantillon ?

3. Pourquoi la marge d’erreur influence-t-elle la taille d’échantillon ?

4. La taille de la population influence-t-elle la taille d’échantillon ?

5. Quelle différence entre taille d’échantillon et puissance statistique ?

6. Comment éviter un échantillon biaisé ?

Rédigé par :

David BOURG Directeur d’études à l’institut Sphinx Domaines d’expertise : pilotage des projets d’études, conseils. David est diplômé du Master Marketing Quantitatif de l’IAE de Grenoble. Il a près de 20 ans d’expérience dans les études marketing acquise en institut d’études en menant des projets auprès de grands groupes (dans le secteur des services notamment : Banque, Assurances, Telecom…), Son rôle au quotidien : définir et piloter les projets d’études permettant à ses clients de prendre des décisions et de définir leur stratégie marketing. Il formule des recommandations suite aux problématiques soulevées par l’étude et apporte son expertise à ses clients.